 login/create account
login/create account
Recent Activity
Call Of Duty Mobile Generator Cheats No Human Verification (Without Surveys) ★★
Author(s):
Call Of Duty Mobile Generator Cheats No Human Verification (Without Surveys)
Keywords:
Family Island Generator Cheats 2024 Generator Cheats Tested On Android Ios (extra) ★★
Author(s):
Family Island Generator Cheats 2024 Generator Cheats Tested On Android Ios (extra)
Keywords:
SimCity BuildIt Generator Cheats Unlimited Resources No Jailbreak (Premium Orginal Generator) ★★
Author(s):
SimCity BuildIt Generator Cheats Unlimited Resources No Jailbreak (Premium Orginal Generator)
Keywords:
PK XD Generator Cheats 2024 Generator Cheats Tested On Android Ios (WORKING TIPS) ★★
Author(s):
PK XD Generator Cheats 2024 Generator Cheats Tested On Android Ios (WORKING TIPS)
Keywords:
MovieStarPlanet Generator Cheats 2024 (WORKING IN 5 SECOND) ★★
Author(s):
MovieStarPlanet Generator Cheats 2024 (WORKING IN 5 SECOND)
Keywords:
Raid Shadow Legends Generator Cheats Free 2024 in 5 minutes (New Generator Cheats Raid Shadow Legends) ★★
Author(s):
Raid Shadow Legends Generator Cheats Free 2024 in 5 minutes (New Generator Cheats Raid Shadow Legends)
Keywords:
Chords of longest cycles ★★★
Author(s): Thomassen
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. Keywords: chord; connectivity; cycle
Do any three longest paths in a connected graph have a vertex in common? ★★
Author(s): Gallai
Keywords:
Chromatic number of $\frac{3}{3}$-power of graph ★★
Author(s):
Let  be a graph and
be a graph and 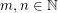 . The graph
. The graph 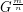 is defined to be the
is defined to be the  -power of the
-power of the  -subdivision of
-subdivision of  . In other words,
. In other words, 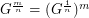 .
.
 be a graph with
be a graph with 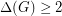 . Then
. Then 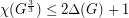 .
. Keywords:
3-Edge-Coloring Conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
 with
with 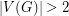 is a connected cubic graph admitting a
is a connected cubic graph admitting a 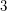 -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 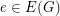 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 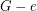 has a
has a 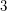 -edge coloring.
-edge coloring. Keywords: 3-edge coloring; 4-flow; removable edge
r-regular graphs are not uniquely hamiltonian. ★★★
Author(s): Sheehan
 is a finite
is a finite  -regular graph, where
-regular graph, where 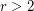 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. Keywords: hamiltonian; regular; uniquely hamiltonian
Partition of Complete Geometric Graph into Plane Trees ★★
Author(s):
Keywords: complete geometric graph, edge colouring
Smooth 4-dimensional Poincare conjecture ★★★★
Author(s): Poincare; Smale; Stallings
 -manifold has the homotopy type of the
-manifold has the homotopy type of the  -sphere
-sphere 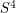 , is it diffeomorphic to
, is it diffeomorphic to 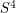 ?
?
Keywords: 4-manifold; poincare; sphere
Book Thickness of Subdivisions ★★
Author(s): Blankenship; Oporowski
Let  be a finite undirected simple graph.
be a finite undirected simple graph.
A  -page book embedding of
-page book embedding of  consists of a linear order
consists of a linear order 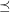 of
of 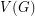 and a (non-proper)
and a (non-proper)  -colouring of
-colouring of 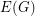 such that edges with the same colour do not cross with respect to
such that edges with the same colour do not cross with respect to 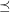 . That is, if
. That is, if 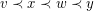 for some edges
for some edges  , then
, then  and
and 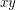 receive distinct colours.
receive distinct colours.
One can think that the vertices are placed along the spine of a book, and the edges are drawn without crossings on the pages of the book.
The book thickness of  , denoted by bt
, denoted by bt is the minimum integer
is the minimum integer  for which there is a
for which there is a  -page book embedding of
-page book embedding of  .
.
Let 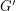 be the graph obtained by subdividing each edge of
be the graph obtained by subdividing each edge of  exactly once.
exactly once.
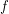 such that for every graph
such that for every graph  ,
, 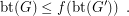
Keywords: book embedding; book thickness
Primitive pythagorean n-tuple tree ★★
Author(s):
Keywords:
Jacobian Conjecture ★★★
Author(s): Keller
 be a field of characteristic zero. A collection
be a field of characteristic zero. A collection 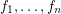 of polynomials in variables
of polynomials in variables 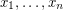 defines an automorphism of
defines an automorphism of 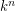 if and only if the Jacobian matrix is a nonzero constant.
if and only if the Jacobian matrix is a nonzero constant. Keywords: Affine Geometry; Automorphisms; Polynomials
Inscribed Square Problem ★★
Author(s): Toeplitz
Keywords: simple closed curve; square
Complete bipartite subgraphs of perfect graphs ★★
Author(s): Fox
 be a perfect graph on
be a perfect graph on  vertices. Is it true that either
vertices. Is it true that either  or
or 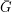 contains a complete bipartite subgraph with bipartition
contains a complete bipartite subgraph with bipartition 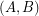 so that
so that 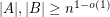 ?
? Keywords: perfect graph
Transversal achievement game on a square grid ★★
Author(s): Erickson
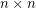 grid. The first player (if any) to occupy a set of
grid. The first player (if any) to occupy a set of  cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play? Keywords: game

 Drupal
Drupal CSI of Charles University
CSI of Charles University