 login/create account
login/create account
Recent Activity
Refuting random 3SAT-instances on $O(n)$ clauses (weak form) ★★★
Author(s): Feige
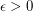 and every rational
and every rational  , there is no polynomial-time algorithm for the following problem.
, there is no polynomial-time algorithm for the following problem.
Given is a 3SAT (3CNF) formula 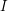 on
on  variables, for some
variables, for some  , and
, and  clauses drawn uniformly at random from the set of formulas on
clauses drawn uniformly at random from the set of formulas on  variables. Return with probability at least 0.5 (over the instances) that
variables. Return with probability at least 0.5 (over the instances) that 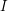 is typical without returning typical for any instance with at least
is typical without returning typical for any instance with at least 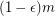 simultaneously satisfiable clauses.
simultaneously satisfiable clauses.
Keywords: NP; randomness in TCS; satisfiability
Does the chromatic symmetric function distinguish between trees? ★★
Author(s): Stanley
Keywords: chromatic polynomial; symmetric function; tree
Shannon capacity of the seven-cycle ★★★
Author(s):
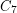 ?
? Keywords:
Magic square of squares ★★
Author(s): LaBar
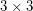 magic square composed of distinct perfect squares?
magic square composed of distinct perfect squares? Keywords:
Inverse Galois Problem ★★★★
Author(s): Hilbert
 .
. Keywords:
Seymour's r-graph conjecture ★★★
Author(s): Seymour
An  -graph is an
-graph is an  -regular graph
-regular graph  with the property that
with the property that 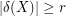 for every
for every 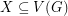 with odd size.
with odd size.
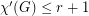 for every
for every  -graph
-graph  .
. Keywords: edge-coloring; r-graph
Edge list coloring conjecture ★★★
Author(s):
 be a loopless multigraph. Then the edge chromatic number of
be a loopless multigraph. Then the edge chromatic number of  equals the list edge chromatic number of
equals the list edge chromatic number of  .
. Keywords:
Kneser–Poulsen conjecture ★★★
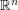 is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease.
is rearranged so that the distance between each pair of centers does not decrease, then the volume of the union of the balls does not decrease. Keywords: pushing disks
Wide partition conjecture ★★
Keywords:
3-accessibility of Fibonacci numbers ★★
Keywords: Fibonacci numbers; monochromatic diffsequences
Simplexity of the n-cube ★★★
Author(s):
 -cube into
-cube into  -simplices?
-simplices? Keywords: cube; decomposition; simplex
Crossing sequences ★★
Author(s): Archdeacon; Bonnington; Siran
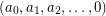 be a sequence of nonnegative integers which strictly decreases until
be a sequence of nonnegative integers which strictly decreases until  .
.
Then there exists a graph that be drawn on a surface with orientable (nonorientable, resp.) genus 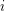 with
with 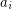 crossings, but not with less crossings.
crossings, but not with less crossings.
Keywords: crossing number; crossing sequence
The Crossing Number of the Complete Graph ★★★
Author(s):
The crossing number 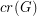 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
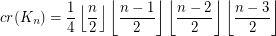
Keywords: complete graph; crossing number
The Crossing Number of the Hypercube ★★
The crossing number 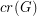 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
The  -dimensional (hyper)cube
-dimensional (hyper)cube  is the graph whose vertices are all binary sequences of length
is the graph whose vertices are all binary sequences of length  , and two of the sequences are adjacent in
, and two of the sequences are adjacent in  if they differ in precisely one coordinate.
if they differ in precisely one coordinate.

Keywords: crossing number; hypercube
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament
Rank vs. Genus ★★★
Author(s): Johnson
Keywords:
The Hodge Conjecture ★★★★
Author(s): Hodge
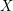 be a complex projective variety. Then every Hodge class is a rational linear combination of the cohomology classes of complex subvarieties of
be a complex projective variety. Then every Hodge class is a rational linear combination of the cohomology classes of complex subvarieties of 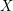 .
. Keywords: Hodge Theory; Millenium Problems
2-accessibility of primes ★★
Keywords: monochromatic diffsequences; primes
Non-edges vs. feedback edge sets in digraphs ★★★
Author(s): Chudnovsky; Seymour; Sullivan
For any simple digraph  , we let
, we let 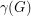 be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and
be the number of unordered pairs of nonadjacent vertices (i.e. the number of non-edges), and 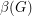 be the size of the smallest feedback edge set.
be the size of the smallest feedback edge set.
 is a simple digraph without directed cycles of length
is a simple digraph without directed cycles of length 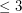 , then
, then 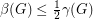 .
. Keywords: acyclic; digraph; feedback edge set; triangle free

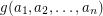 of co-prime positive integers
of co-prime positive integers 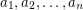 for
for 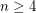 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University