 login/create account
login/create account
Recent Activity
Subset-sums equality (pigeonhole version) ★★★
Author(s):
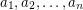 be natural numbers with
be natural numbers with 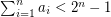 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 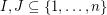 with
with 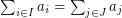 . Is it possible to find such a pair
. Is it possible to find such a pair 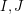 in polynomial time?
in polynomial time? Keywords: polynomial algorithm; search problem
Weak pentagon problem ★★
Author(s): Samal
 is a cubic graph not containing a triangle, then it is possible to color the edges of
is a cubic graph not containing a triangle, then it is possible to color the edges of  by five colors, so that the complement of every color class is a bipartite graph.
by five colors, so that the complement of every color class is a bipartite graph. Keywords: Clebsch graph; cut-continuous mapping; edge-coloring; homomorphism; pentagon
Lonely runner conjecture ★★★
 runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least
runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least  (along the track) away from every other runner.
(along the track) away from every other runner. Keywords: diophantine approximation; view obstruction
Mapping planar graphs to odd cycles ★★★
Author(s): Jaeger
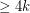 has a homomorphism to
has a homomorphism to 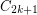 .
. Keywords: girth; homomorphism; planar graph
5-local-tensions ★★
Author(s): DeVos
 (probably
(probably 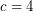 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 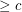 has a 5-local-tension.
has a 5-local-tension. Concavity of van der Waerden numbers ★★
Author(s): Landman
For  and
and 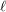 positive integers, the (mixed) van der Waerden number
positive integers, the (mixed) van der Waerden number 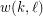 is the least positive integer
is the least positive integer  such that every (red-blue)-coloring of
such that every (red-blue)-coloring of ![$ [1,n] $](/files/tex/661d0acc09fbc5b62f49645a71cf7d831a26563f.png) admits either a
admits either a  -term red arithmetic progression or an
-term red arithmetic progression or an 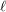 -term blue arithmetic progression.
-term blue arithmetic progression.
 and
and 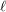 with
with 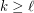 ,
, 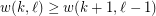 .
. Keywords: arithmetic progression; van der Waerden
Circular coloring triangle-free subcubic planar graphs ★★
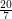 ?
? Keywords: circular coloring; planar graph; triangle free
List colorings of edge-critical graphs ★★
Author(s): Mohar
 is a
is a  -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 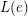 of
of  colors. Then
colors. Then  is
is  -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other. Keywords: edge-coloring; list coloring
Aharoni-Berger conjecture ★★★
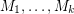 are matroids on
are matroids on  and
and 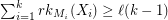 for every partition
for every partition  of
of  , then there exists
, then there exists 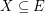 with
with 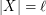 which is independent in every
which is independent in every 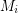 .
. Keywords: independent set; matroid; partition
The large sets conjecture ★★★
Author(s): Brown; Graham; Landman
 is 2-large, then
is 2-large, then  is large.
is large. Keywords: 2-large sets; large sets
Ramsey properties of Cayley graphs ★★★
Author(s): Alon
 so that every abelian group
so that every abelian group  has a subset
has a subset 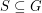 with
with 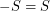 so that the Cayley graph
so that the Cayley graph 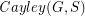 has no clique or independent set of size
has no clique or independent set of size 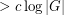 .
. Keywords: Cayley graph; Ramsey number
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 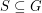 let
let 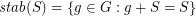 .
.
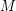 be a matroid on
be a matroid on  , let
, let 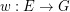 be a map, put
be a map, put 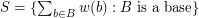 and
and 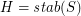 . Then
. Then 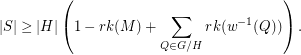
The Erdos-Turan conjecture on additive bases ★★★★
Let 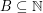 . The representation function
. The representation function 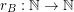 for
for 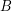 is given by the rule
is given by the rule 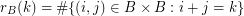 . We call
. We call 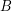 an additive basis if
an additive basis if 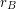 is never
is never  .
.
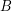 is an additive basis, then
is an additive basis, then 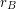 is unbounded.
is unbounded. Keywords: additive basis; representation function
Rota's unimodal conjecture ★★★
Author(s): Rota
Let 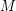 be a matroid of rank
be a matroid of rank  , and for
, and for 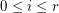 let
let 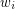 be the number of closed sets of rank
be the number of closed sets of rank 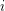 .
.
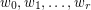 is unimodal.
is unimodal. 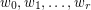 is log-concave.
is log-concave. Keywords: flat; log-concave; matroid
A conjecture on iterated circumcentres ★★
Author(s): Goddyn
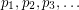 be a sequence of points in
be a sequence of points in 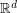 with the property that for every
with the property that for every 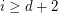 , the points
, the points 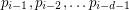 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 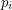 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 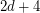 ?
? Keywords: periodic; plane geometry; sequence
Unions of triangle free graphs ★★★
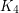 which cannot be expressed as a union of
which cannot be expressed as a union of 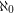 triangle free graphs?
triangle free graphs? Keywords: forbidden subgraph; infinite graph; triangle free
The Two Color Conjecture ★★
Author(s): Neumann-Lara
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 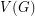 into
into 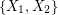 so that the graph induced by
so that the graph induced by 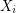 is acyclic for
is acyclic for 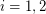 .
. Half-integral flow polynomial values ★★
Author(s): Mohar
Let 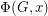 be the flow polynomial of a graph
be the flow polynomial of a graph  . So for every positive integer
. So for every positive integer  , the value
, the value 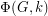 equals the number of nowhere-zero
equals the number of nowhere-zero  -flows in
-flows in  .
.
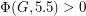 for every 2-edge-connected graph
for every 2-edge-connected graph  .
. Keywords: nowhere-zero flow
Gao's theorem for nonabelian groups ★★
Author(s): DeVos
For every finite multiplicative group  , let
, let 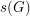 (
(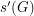 ) denote the smallest integer
) denote the smallest integer  so that every sequence of
so that every sequence of  elements of
elements of  has a subsequence of length
has a subsequence of length 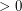 (length
(length 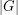 ) which has product equal to 1 in some order.
) which has product equal to 1 in some order.
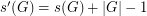 for every finite group
for every finite group  .
. Keywords: subsequence sum; zero sum
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 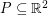 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in 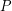 , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
 -universal set of size
-universal set of size 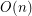 ?
? Keywords: geometric graph; planar graph; universal set

 Drupal
Drupal CSI of Charles University
CSI of Charles University